損益曲線とリスク指標曲線についての覚書｜りゅう先生講義録９

スポンサーリンク

ある日の後場、いつものごとく（？）相場が横横を繰り返しているとき、りゅう式オプショントレードを習得するために組んでみた、オプションのバーチャルポジションに関してりゅう先生にあれこれ質問をしていると、そのポジションのデルタ、ガンマ、セータ、ベガの各リスク指標の時間経過による曲線の変化が分かるグラフを描いてみてごらんと言われました。

えっ、何それ？と、一瞬思いましたが、それってどんなグラフなんだろうという好奇心もあって、急ぎプログラミングをして、そのグラフを描いてみることにしました。

オプションの本を何冊か読みはしましたが、そのようなグラフを見た記憶がなく、どのようなグラフができるのかとちょっとわくわくしながら、プログラミングを急ぎました。そして、出来上がったのが、次の図１から図５の各グラフです。

ここでは、バーチャのポジの各指標曲線ではなく、話を分かりやすくするために、ロングストラドルの例でそれら曲線を描いています。さらに、グラフを見やすくするために、玉の建値は１００円にし、オプション価格、IV、原資産価格、オプションの残存日数などは、日経２２５オプションの２０１９年１０月限の２０１９年9月１７日の終値を用いて描いています。

例：ロングストラドル
C２１５００　５２５円、買い１枚（建値　１００円）
P２１５００　２００円、買い１枚（建値　１００円）

図１　損益曲線（縦軸：損益、横軸：権利行使価格）

図２　デルタ曲線

図３　ガンマ曲線

図４　セータ曲線

図５　ベガ曲線

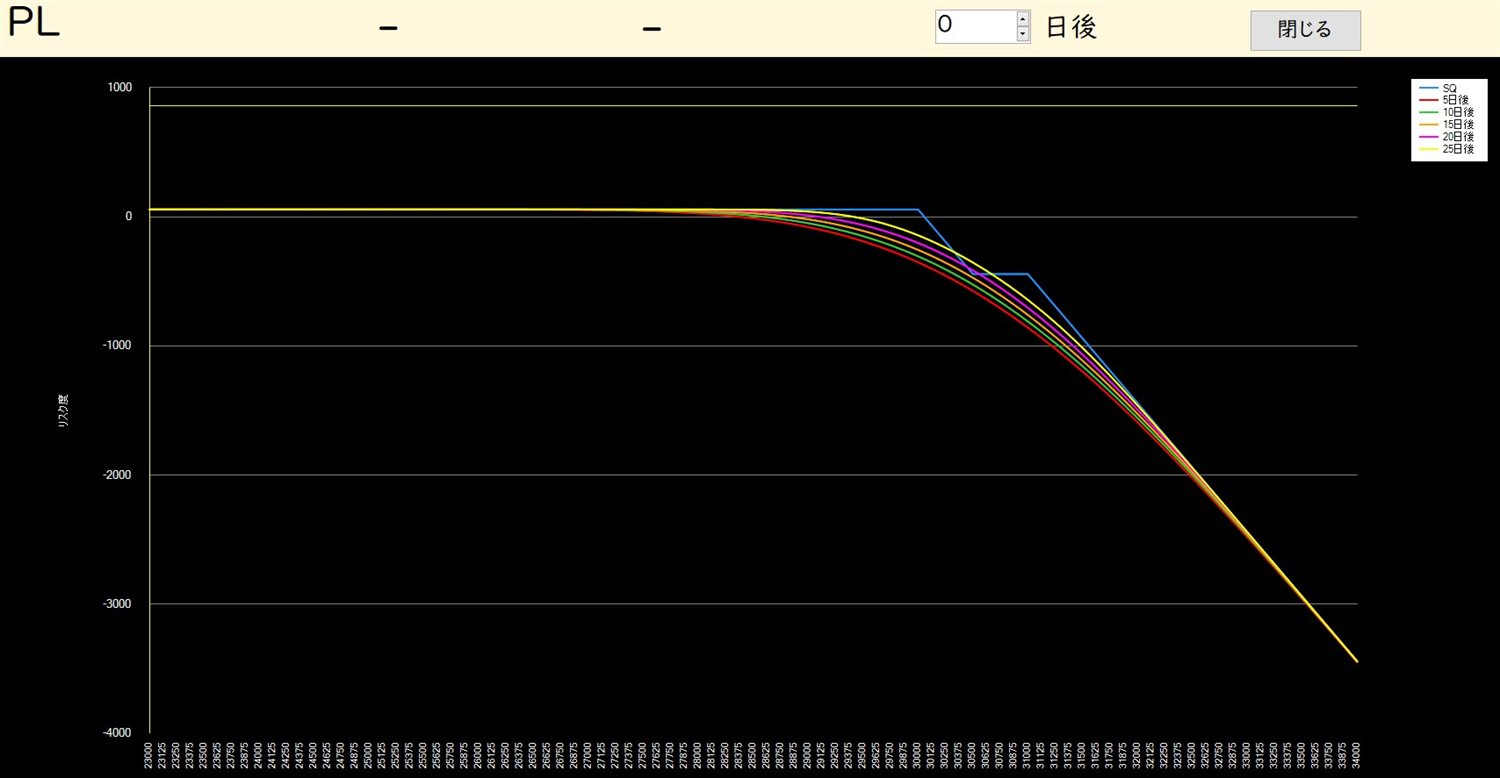
図１はこのロングストラドルの満期と期中の損益曲線です。このグラフは、オプション関係の本やインターネット上のオプションサイトなどで普通に見ることができるもので、ここでこのグラフの見方を詳細に説明する必要はないでしょう。私も図1のグラフはよく見ていたので、これについては特に問題もなく、自分のバーチャポジションの損益曲線を日々眺めていました。

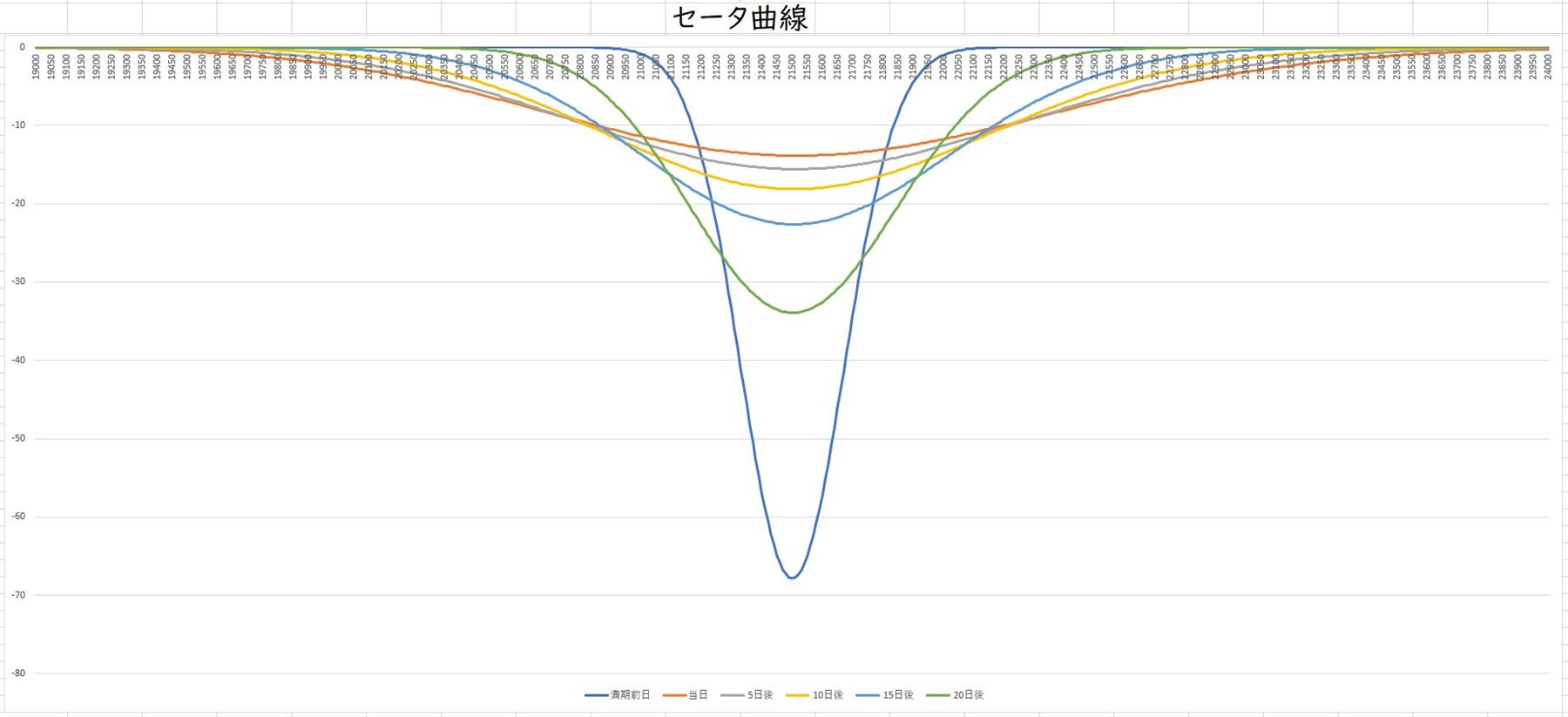
しかし、図2から図５の各リスク指標の曲線はこのグラフを描くまで一度も見たことがなく、自分でこれらのグラフを描いたものの、それらグラフをどのように見て、何をどう判断すれば、いいのか、さっぱり分かりませんでした。

とりあえず、急ぎグラフが出来上がったので、りゅう先生に見せると（実際にお見せしたグラフはこれらのグラフではないが）、ポジションのリスクがよく分かるねと言われました。

それを聞いた私は、どうしてこれらのグラフを見て、それが分かるのか不思議でたまりませんでした。

それから、しばらくこのグラフの見方がよく分からないまま悶々とした日々を過ごしているとき、https://ps.nikkei.co.jp/jpx2019/strategy13.htmlの記事中に掲載されていた図を見て、なるほど、そういうことだったのかと気づき、次の図６のように考えると、各リスク指標曲線の意味がよく理解できることが分かりました。

図6　図１の損益曲線の一部を拡大

この図６にはデルタ、ガンマ、セータが表わす指標の意味を書き加えていますが、これを見ると、各指標曲線が何を表わしているかがよく分かります。

図６の損益曲線においてデルタは曲線の傾きで、デルタが中央で±ゼロ、右側がデルタプラスの領域で、左側がデルタマイナスの領域を表わしています。このことを理解した上で、図２のデルタ曲線を見ると、デルタ０のところを境にして上側がデルタプラスの領域、下側がデルタマイナスの領域となっていますが、その意味するところは、図６のグラフの傾きの大きさであることがすぐに理解できます。

そして、図６のグラフにおいてガンマは上向きの力、セータは下向きの力とみることができ、ガンマとセータが真逆のグラフになっている理由がこのグラフを見ると、よく理解できるでしょう。図３と図4のグラフを見比べてみて下さい。つまり、ガンマとセータは常に綱引きの関係にあることが分かります。

相場が上下にほとんど動かず、原資産価格が同じところにとどまっていると、セータの下向きの力によって日に日にこのポジションの損益が落ちてくることが、この図6を見ると、よく分かります。まるで重力のような存在です。そのため、その下向きの力に逆らうガンマのような上向きの力を加えない限り、自然と下に落ちていく、つまり、損益が日に日に減っていくわけです。これは、今回のポジションがそのような状況になるだけで、ポジションによって、たとえば、ショートポジションの場合、これとは逆になります。つまり、セータが上向きの力となります。

さて、残ったベガですが、このベガをこの図６においてどのように描けばよいのか、よく分かりませんでしたので、ベガを描いていません。

図５のベガのグラフと、図１の損益曲線とを比較すると、ベガの値が小さいほど、利益が大きくなっていることが分かります。つまり、このポジションの場合、ベガによる影響がほぼない領域で利益が増えていくことが分かります。

ベガはIVが１％上昇したときのオプション価格の変化量を表わすので、ベガが０に近づくほどベガによるオプション価格への影響がほとんどなくなり、IVによる影響が大きくなるということが分かります。つまり、オプション価格はIVの影響を受けやすくなるということです。

では、図6においてベガを描けなかった私は、自分がポジションを持った時、ベガの影響がどのようにポジションに影響してくるのか、どうすれば、それが分かるのかと、りゅう先生に尋ねてみると、

「経験です。程度の差こそあれ実弾突っ込めば、（ベガの影響を実感することを）すぐ経験でしますよ。」

と優しく（？）答えが返ってきました。

実際に経験してこそ理解できるベガって、掴みどころがないやっちゃなあと、私は思うのでした。いつの日か、ベガを理解できる日が来るのでしょうか。

このベガについては、私の理解が進んだ時、また改めて記事を書きたいと思います。いつになるやら。(笑)

スポンサーリンク